Transition à la turbulence en régime hypersonique : comment modéliser les pointes avant des véhicules spatiaux ?

L’accès à l’espace implique la traversée de l’atmosphère terrestre. Une rentrée hypersonique est éprouvante, le frottement des véhicules sur l’air induisant une ablation de ses couches de protection thermique. Pour en limiter les effets, il faut limiter les flux de chaleur pariétaux. Dans les phases denses de l’atmosphère, une couche limite se forme autour du véhicule. Elle est d'abord laminaire et les molécules d’air y suivent la géométrie de la paroi. Lors de la descente, elle évolue vers un état de turbulence développée, le mouvement de ces particules devenant chaotique. Les flux de chaleur pariétaux sont alors plusieurs fois supérieurs à ceux de la couche laminaire. Un processus complexe de transition à la turbulence dimensionne donc le design des protections thermiques. Des chercheurs du CEA - DAM, de l’Institut Pprime et de l’université de San Diego, aux États-Unis, ont entrepris d’en décoder les mécanismes, entrevoyant les raisons d’un phénomène propre aux géométries émoussées, observé depuis plus d’un demi-siècle.

L’objectif principal est alors d’explorer quel est le mécanisme sous-jacent à l’amplification des perturbations près du point d’arrêt, à l’avant des corps arrondis. Pour ce faire, les effets des nombres de Reynolds et de Mach, deux paramètres clés qui influencent le comportement des écoulements, ont été examinés (figure 1). En particulier, les auteurs ont cherché à identifier les tendances associées à ces paramètres et à comprendre comment elles affectent l’amplification des perturbations menant à la turbulence.

Les équations de Navier-Stokes sont l’outil principal pour décrire ces écoulements fortement compressibles. La résolution numérique de ces équations sur un maillage suffisamment fin pour capturer les plus petites structures de turbulence (simulation de haute fidélité constituant une véritable expérimentation numérique et nécessitant des moyens de calcul adéquats) est la première étape de l’étude. L’idée (figure 2) est ensuite de décomposer localement l’écoulement q en la somme d’un écoulement stationnaire q0 et d’une petite perturbation harmonique q′. La linéarisation des équations de Navier-Stokes au voisinage de q0 fait apparaître la matrice jacobienne Jq0 dont dépend l’évolution de q′. Dans le cas où cette petite perturbation est conditionnée par un forçage instationnaire extérieur fext de faible amplitude, la transposition de (1) dans l’espace fréquentiel (éq. 2) prend la forme d’un système entrée-sortie : le forçage fext produit une réponse q′ par action de la fonction de transfert R(ω), dite matrice résolvante. Une approche de haute fidélité basée sur l’analyse de la matrice résolvante permet alors de répondre à la question suivante : quelles sont les perturbations fext de l’écoulement qui vont causer les réponses q′ d’énergie maximale ?

La décomposition de la résolvante R(ω) en valeurs singulières (SVD) permet de déterminer quelles structures pilotent la dynamique de l’écoulement à la fréquence ω. Parmi ces structures, les forçages optimaux fopt décrivent les supports physiques linéairement indépendants qui peuvent recevoir l’énergie des perturbations extérieures par projection de fext, c’est le processus dit de réceptivité. Cette décomposition de la résolvante permet également de déterminer quelles structures, nommées réponses optimales qopt, sont susceptibles de s’amplifier indépendamment dans l’écoulement. Enfin, l’importance de chacune de ces structures optimales est donnée par les gains optimaux Gi qui leur sont associés. L’amplitude relative de ces gains détermine si un seul (G0 >> G1) ou au contraire plusieurs mécanisme(s) domineront la dynamique de l’écoulement.

En utilisant cette méthode, nous pouvons prévoir quelles perturbations sont potentiellement les plus problématiques et quelles réponses elles engendrent. Ainsi, l’écoulement a été modélisé autour d’un corps de forme parabolique, simple, mais représentative des corps arrondis. Les simulations ont été réalisées pour une gamme de nombres de Reynolds (de 100 à 300 000, basé sur le rayon de la pointe avant) et de nombres de Mach (de 0,3 à 1,2), couvrant ainsi une large gamme de conditions d’écoulement du régime incompressible à compressible, jusqu’au supersonique.

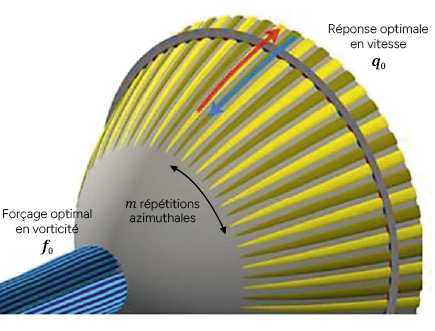
Les résultats ont révélé que l’amplification maximale des réponses se produit pour des perturbations de fréquence nulle, ce qui suggère que les perturbations de basse fréquence jouent un rôle crucial dans la transition vers la turbulence. En d’autres termes, même de petites fluctuations lentes dans l’écoulement peuvent avoir un impact significatif. Les modes de forçage et de réponse optimaux ont montré un mécanisme de réceptivité associé à la vorticité de l’écoulement libre qui pénètre dans la couche limite près du point d’arrêt et exploite un soulèvement de l’écoulement lent proche de la paroi (lift-up) pour créer des structures en stries à la surface du corps (figure 3).

Ces résultats ont des implications importantes pour la conception des véhicules. Comprendre comment les perturbations sont amplifiées autour des corps arrondis permet de mieux prédire la transition vers la turbulence et, par conséquent, d’optimiser la forme des corps pour minimiser la traînée et le transfert de chaleur.